Limite:
Decimos que el límite de f(x) cuando x tiende al punto a es L si la función toma valores cada vez más cercanos a L cuando x toma valores cada vez más cercanos al punto a.
Lo expresamos mediante
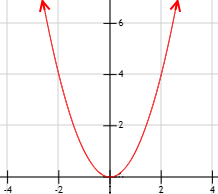
Consideremos la función f(x) = x 2. Para calcular su límite en el punto x = 2, damos a x valores cercanos a 2 por su izquierda y su derecha.
Por la izquierda:
Por la derecha:
Se observa que la función tiende a 4 por ambos lados de 2. Por tanto, su límite es 4:
Gráfica de la función:
Numero "e":
El número e debe su nombre a sus descubridores ya que en algunas ocasiones podemos encontrar este número de la forma número de Euler (Leonhard Euler) o constante de Napier (John Napier).
El número e y los límites
Tenemos que pensar en un límite de una función determinada cuando queramos entender el origen matemático del número e:
Esta función es una sucesión tal que:

Hablamos de sucesión porque podemos asignar valores ordenados a la variable n.
Para n=1 tendremos f(1) = 2
Para n= 20 tendremos f(20) = 2,65329
Para n=100 tendremos f(100) = 2,7048
Podéis ver que a medida que incrementamos el valor de n, es decir, incrementamos la longitud de la sucesión, más se acerca el resultado de la función al número e. ¿Qué pasará para n = 10 000?
Para n= 10 000 tendremos f(10 000) = 2,718146
La expresión matemática generalizada de la sucesión sería teniendo en cuenta que n se aproxima a infinito. En el siguiente gráfico se puede ver como la sucesión (línea negra) va acercándose al límite (línea azul), es decir, al número e, a medida que aumenta n.

Entonces, podemos entender el número e como un límite de una sucesión:
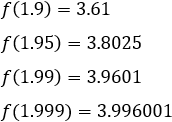
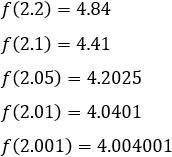


No hay comentarios.:
Publicar un comentario