Cramer

 Tenemos un sistema de Cramer, como por ejemplo el siguiente:

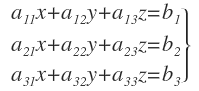
Para hallar la solución de cada una de las incógnitas, debemos dividir el determinante asociado a cada incógnita (que veremos más adelante cómo se calcula) entre el determinante de la matriz de los coeficientes.

De esta forma, la incógnita «x» es igual al determinante asociado a «x» entre el determinante de la matriz de los coeficientes:

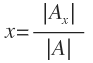
La incógnita «y» es igual al determinante asociado a «y» entre el determinante de la matriz de los coeficientes:

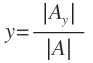
Y la incógnita «z» es igual al determinante asociado a «z» entre el determinante de la matriz de los coeficientes:

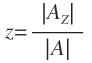
Donde como sabemos, el determinante de la matriz de los coeficientes es:

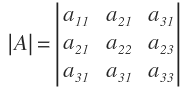
Para obtener el determinante asociado a «x», en la matriz de los coeficientes, sustituimos la primera columna, que es la que corresponde a la incógnita «x», por la columna que forman los términos independientes:

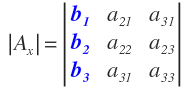
Para obtener el determinante asociado a «y» procedemos de forma similar: en la matriz de los coeficientes, sustituimos la segunda columna, que es la que corresponde a la incógnita «y», por la columna que forman los términos independientes:

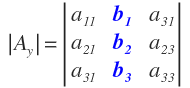
Y para obtener el determinante asociado a «z», en la matriz de los coeficientes, sustituimos la tercera columna, que es la que corresponde a la incógnita «z», por la columna que forman los términos independientes:

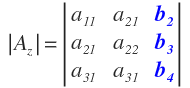
Hemos visto cómo se resuelve, en general, un sistema 3×3 con la regla de Cramer. Para sistemas 2×2, 4×4 o mayores, se procedería de la misma forma.